사이클로이드는 바퀴라는 의미의 그리스어에서 나온 말로 회전하는 바퀴상의 한 점의 궤적을 나타낸다. 예를 들어 퀵보드 바퀴의 한 지점에 발광 다이오드를 붙여 B셔트 촬영을 한다면 사진에는 호빵 모양의 곡선이 나타나게 되는데 이것이 사이클로이드이다. 바퀴가 앞으로 진행해 갈 때 발광다이오드를 붙인 지점이 따라 움직이면서 만드는 곡선이 ‘사이클로이드’인 것이다.
사이클로이드는 룰렛(커브 위에 다른 커브를 돌리면 나오는 커브)의 일종이다.
사이클로이드는 17세기 수학자들 사이에서 빈번히 논쟁을 야기하여 헬렌의 기하학이라고 불린다. 수학의 역사가들은 사이클로이드의 발견자로 여러 후보자들을 제안하였다. 수학역사학자 Paul Tannery는 대표적인 시리아 철학자인 Iamblichus의 연구를 고대에 잘 알려져 있던 곡선의 증거로써 비슷하게 인용했다.
영국의 수학자 존 월리스가 1679년에 쓴 글은 Nicholas of Cusa의 발견에 기여했다. 그러나 이후에 학문은 월리스가 잘못했거나 월리스가 사용한 증거가 이제는 사라졌음을 나타낸다.
갈릴레오 갈릴레이의 이름은 19세기 말에 등장하였고 적어도 한명의 저자는 Marin Mersenne에게도 공이 있다는 것을 보고했다. Moritz Cantor와 Siegmund Günther의 연구를 시작으로, 이제 학자들은 1503년에 출판된 기하학의 기초에서 프랑스 수학자인 Charles de Bovelles가 설명한 사이클로이드를 가장 우선적이라고 정한다. 이러한 연구에서, Bovelles는 작은 원보다 120퍼센트 더 큰 반지름의 일부를 원을 굴려 남은 자취의 곡선으로 오해했다.

갈릴레오는 사이클로이드라는 용어를 만들었고 최초로 곡선에 대한 연구를 시작하였다. 그의 제자 에반젤리스타 토리첼리에 따르면, 1599년 갈릴레오는 (사이클로이드 밑의 면적과 같은 면적의 정사각형을 만든) 사이클로이드의 구적법을 판금에 원을 만들고 사이클로이드를 생성하고 그것을 자르고 무게를 재며 자취를 따라가는 비정상적이고 경험적인 접근으로 시도했다. 그는 비율이 대충 3:1이라는 것을 발견했지만 비율이 무리수의 분수로 직교/구적법이 불가능하다고 부정확하게 결론지었다. 1628년경에, Gilles Persone de Roberval은 아마도 Père Marin Mersenne에게 구적법문제를 배웠고 Cavalieri의 이론을 사용함으로써 1634년에 직교/구적법에게 영향을 주었다. 그러나, (Traité des Indivisibles에 있던) 그의 노력은 1693년까지 드러나지 않았다. 사이클로이드의 접선을 그리는 것은 Mersenne이helm Leibniz는 단 하나의 방정식으로 곡선을 설명하기 위해서 분석적인/분해의 기하학을 사용했다. 1696년에는 요한 베르누이(Johann Bernoulli)가 사이클로이드의 의문을 풀어주는 최속 강하선 증명을 사용했다.
시점과 종점이 같은 복수의 직선이나 곡선 중에서, 중력장 내에서 그 위를 물체가 가장 빨리 움직이는 것은 사이클로이드이다.
놀이기구나 미끄럼틀을 보면 가장 최단 거리인 직선이 아닌 곡선 모양으로 돼있음을 볼 수 있다. 실제로 직선 미끄럼틀보다는 곡선 미끄럼틀이 더 빨리 내려오는 이유는 그 곡선이 사이클로이드기 때문이다. 자동차 기어에 쓰이는 톱니바퀴도 마모를 줄이기 위해 사이클로이드 곡선을 이용했다.
우리나라 전통 가옥의 기와에도 아름다운 곡선, 사이클로이드가 숨어있다. 사이클로이드 곡선은 경사면에서 가장 빠른 속도를 내는 특징을 가졌기 때문에 기와에 비를 맞을 경우, 빗방울은 최대한 빨리 기와를 타고 흘러 떨어진다. 빗물이 기와에 스며들 새 없이 흘러버리면 빗물로 인해 목조건물이 썩는 것을 방지할 수 있다. 우리 선조들의 훌륭한 지혜가 숨어있는 것이다.

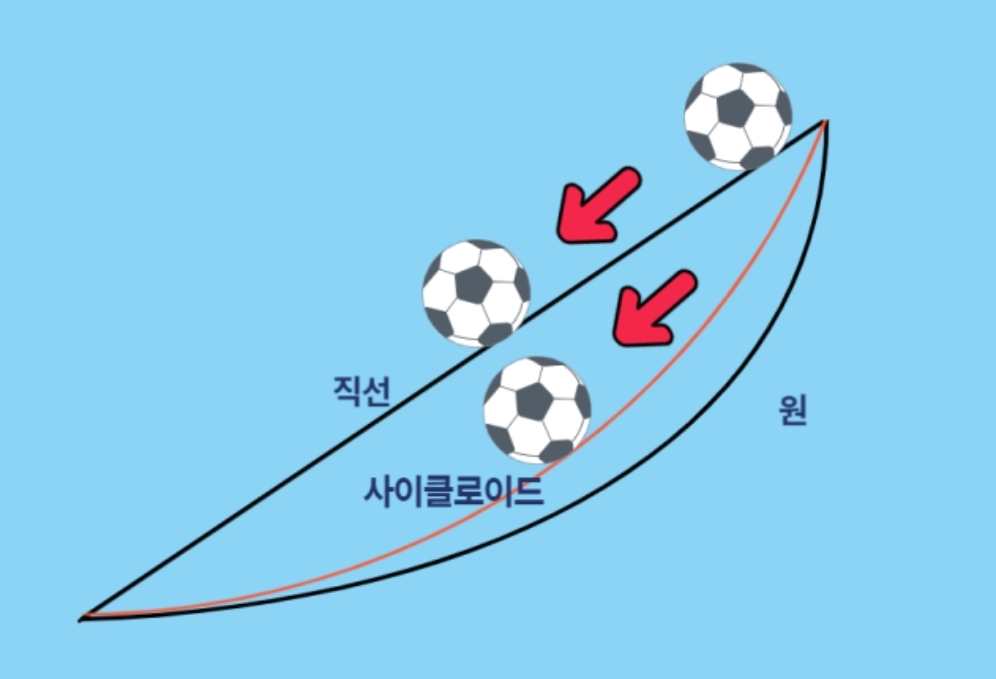
사이클로이드는 대표적으로 2가지 성질이 있다. 첫번째로는 '최단시간강하곡선'이라는 점이다. 이 덕분에 실생활에서 놀이기구나 미끄럼틀이 사이클로이드 곡선으로 이뤄져 있어 더 스릴을 즐길 수 있는 것이다.
또한 중력장 내에서 사이클로이드의 어느 위치에 물체를 강하하기 시작하여도 사이클로이드의 수평의 끝점에 도착하는 시간은 동일하다. 이러한 성질을 나타내는 곡선을 등시곡선(isochrone curve, tautochrone curve)이라고 한다.
1583년 성당에서 예배를 드리던 갈릴레이가 천정에 매달린 진자의 주기가 진폭에 상관없이 일정하다는 ‘진자의 등시성’을 발견했다는 이야기는 너무나 유명하다. 하지만 정확하게 이야기 한다면 등시성(isochronism)은 진자의 진폭이 매우 작을 경우에만 성립한다. 일반적으로 진폭이 커지면 주기도 증가하기 때문에 진자의 등시성은 성립하지 않는데 정밀한 시계가 없었던 당시에는 이러한 사실을 알아내기 어려웠을 것이다.
그런데 네덜란드의 물리학자 호이겐스는 1673년 『진자시계Horologium Oscilatorium』라는 명저를 통해 진자가 호가 아니라 사이클로이드를 따라 움직일 경우에 진자의 궤도가 등시곡선(tautochrone)이 된다는 것을 증명하고, 이러한 성질을 이용해 진자시계를 만들었다. 그의 진자시계는 두 개의 사이클로이드 벽면(그림1에서 E와 F) 사이에서 진자가 움직이도록 만든 것인데, 이렇게 하면 진자의 움직임도 사이클로이드가 된다.
최단거리를 찾아주는 ‘사이클로이드’
1696년 쟝 베르누이는 유럽의 물리학자들에게 ‘브라키스토크론 (brachistochrone, 그리스어의 가장 짧음을 의미하는 ‘brakistos’와 시간을 의미하는 ‘kronos’를 합친 말로 보통 ‘최속강하선’이라고 불린다) 문제’라는 것을 낸 적이 있었다. 이는 위아래로 떨어진 두 지점 사이에서 어떤 경로를 따라 내려가는 것이 가장 빨리 내려갈 수 있는지를 찾는 것이었다. 흔히 생각하면 직선 경로가 최단 거리이기 때문에 가장 빠를 것 같지만 실상은 사이클로이드 곡선을 따라 내려가는 것이 가장 빠르다. 사이클로이드 위에서는 각 지점에서 중력가속도가 줄어드는 정도가 직선보다 작기 때문에 가속도에 의해 속도가 점점 빨라져서 도착 지점까지의 시간이 직선이나 다른 어떤 궤적 보다 빠른 것이다. 즉 풀장의 미끄럼틀도 놀이터에 있는 것과 같은 직선 형태로 만드는 것보다 사이클로이드 형태로 만들게 되면 더 빨리 내려오기 때문에 더 큰 스릴을 맛볼 수 있는 것이다. (그림2에서 보면 A에서 동시에 출발한 연두색 공과 파란색 공은 파란색 공이 연두색 공보다 더 먼 거리를 이동함에도 불구하고 B지점에 먼저 도착하게 된다).
이 문제를 최초로 풀어낸 것은 베르누이 형제였으며, 이후 뉴턴과 라이프니츠, 로비탈이 풀이에 성공했다고 한다. 전해지는 바에 의하면 당시 많은 물리학자들이 몇 달 동안 이 문제를 풀기 위해 고민했으나 뉴턴은 단 하루 만에 풀어 버렸다고 하니 과연 뉴턴은 뛰어난 천재임은 분명한 듯 보인다.
일상에 숨은 ‘사이클로이드’
그런데 뛰어난 물리학자들도 쉽게 풀지 못한 문제를 독수리는 어떻게 알았는지 먹이를 향해 낙하할 때 사이클로이드 곡선 형태에 가깝게 낙하한다. 땅 위에 있는 들쥐나 토끼, 쥐, 뱀 등 먹이를 잡을 때 직선이 아닌, 최단시간이 소요되는 ‘사이클로이드’와 가까운 곡선을 그리며 목표물로 향하는 것이다. 또한 일반 새들도 몸체를 기준으로 날개 끝이 사이크로이드 형태의 타원궤적을 이루며 이로 인한 양력으로 전진하며 물고기의 비늘에도 사이클로이드 곡선이 숨겨져 있다고 하니 자연의 숨겨진 아름다움과 효율성에 앞에 다시 놀라지 않을 수 없다. 이외에 우리나라 전통 가옥의 기와 역시 사이클로이드 곡선 모양을 하고 있어 비로 인한 목조 건물의 부식을 막고 있다. (글 : 최원석 - 과학칼럼니스트)
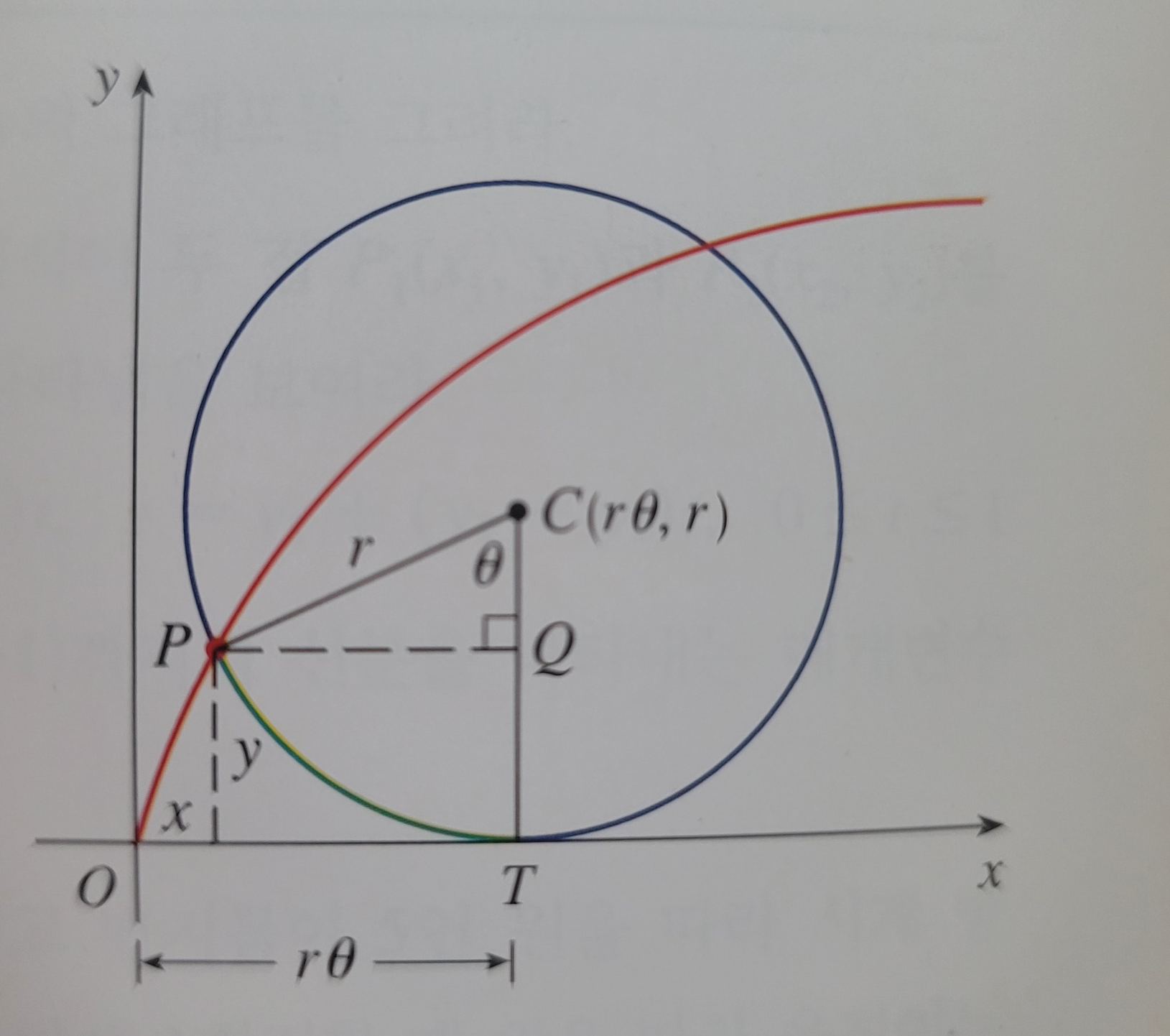
출처:
위키백과
에듀진 기사
KISTI의 과학향기
해롱쌤의 수학이 즐거운 마법 BLOG
