말이 필요없는 증명..
영어 원제는 'proof without words'인데 수학계에서는 PWW라는 약칭으로 불리며
오래전부터 연구되어 온 분야입니다.
PWW(무언증명)는 미국수학협회가 빌행하는 학술지 수학매거진이나 대학 수학저널 등에는
1970년대부터 고정 칼럼으로 기고되고 있는데
'재미있는 그림'만큼이나 수학적 정합성을 흥미롭게 보여주는 형식이 없다고 판단했기 때문입니다.
유명한 수학자이자 과학자인 마틴 가드너는 이 무언증명을 일컬어 다음과 같이 말한 바 있습니다.
"올바른 정리임을한눈에 알아볼 수 있는 매우 단순하며 아름다운 그림으로 기존정리의 증명이
가지는 무미건조함을 보환할수 있다!'
이 말은 눈으로 보고 직관적으로 이해한다는 뜻인거 같습니다..
그렇지만 어떤 의미로 무언증명은 실제 명학한 증명이라 할수 없습니다.
대신 어떤 명제를 증명하기 위해 어떤 단서부터 시작하면 좋을지 혹은 명제를 증명해 가는 과정을 보여 주기 위한
용도로 사용됩니다. 하지만 그렇다고 해도 무언증명의 효능이 간과되어서는 곤란합니다.
무언중명은 수학을 이해하는 데 매우 효과적인 도구로 사용될 수 있기 때문입니다.
그 이유를 한번 살펴볼까요?
통상 공식이나 언어로 증명을 학습하는 과정은 어떻게 진행될까요?
학생들은 위에서 아래로, 혹은 왼쪽에서 오른쪽으로 정해진 순서에 따라 글자(수식)를 읽어 나가면서 증명을 파악해 나갑니다.
이때 수동적으로 임할 수밖에없습니다.
읽어나가는 글자(수식) 틀에 맞취 증명자가 제시하는생각대로 따라가게 되기 때문입니다.
그래서 학생들은 수학의 증명을 싫어하고 지루해하기도 합니다.
그런데 무언증명은 여러 단서를 동시에 담고 있으며 사고의 프로세스를 가뒤두지 않습니다.
어떤 명제가 왜 참인지를 이해하도록 도와줄 뿐 아니라 해당 명제를 증명하기 위해서 어디서부터 어떻게 시작하는 게 좋을지 힌트를 줍니다.
어디서부터 어떻게 시작할지는 무언증명을 보고 실행하는 학습자의 목적입니다.
실제 수학 공부를 할 때 학생들은 다양한 문제들을 직접 풀어나가면서 문제를 해결하는 핵심
아이디어를 스스로 찾아나가게 됩니다. 무언증명 역시 그와 비숫한 쾌감을 맛불 수 있는 증명 이해 방법입니다. 게다가 문제 풀이보다도 더욱 능동적으로 증명을 학습할 수 있는 방편이기도 합니다.
그림의 도움을 받기는 하지만 오롯이 자신의 사고로만 추론하기 때문에, 직접 증명을 해냈다는 성취감도 느낄 수 있습니다. 수학적 사고를 자극하는 여러 그림을 해석해서 증명에 도전해 본다면 시각화 능력, 수학적 직관력, 논리력 등을 다양하게 기를수있을것으로 기대됩니다.
때로는 명제 하나에 여러 그림이 동시에 제공되기도 합니다.
이는 특정 증명에 대해서도 매우 다양한 접근이 가능하다는 것을 경험적으로 체득할 수 있도록 한 장치입니다.
무언증명 풀이탐구
복잡한 증명 대신 무언증명으로 더욱 진관적인 이해를 돕도록 심화학습을 진행한다.
학습 게시판에 주 1회 무언증명을 게시후 증명을 해낸 친구들에게 선물을 주는등 나눔을 한다.
발표 기회가 주어졌을때 스피드 퀴즈등의 방식으로 친구들과 탐구 해결 해 보는것도 재밌을 것이다.
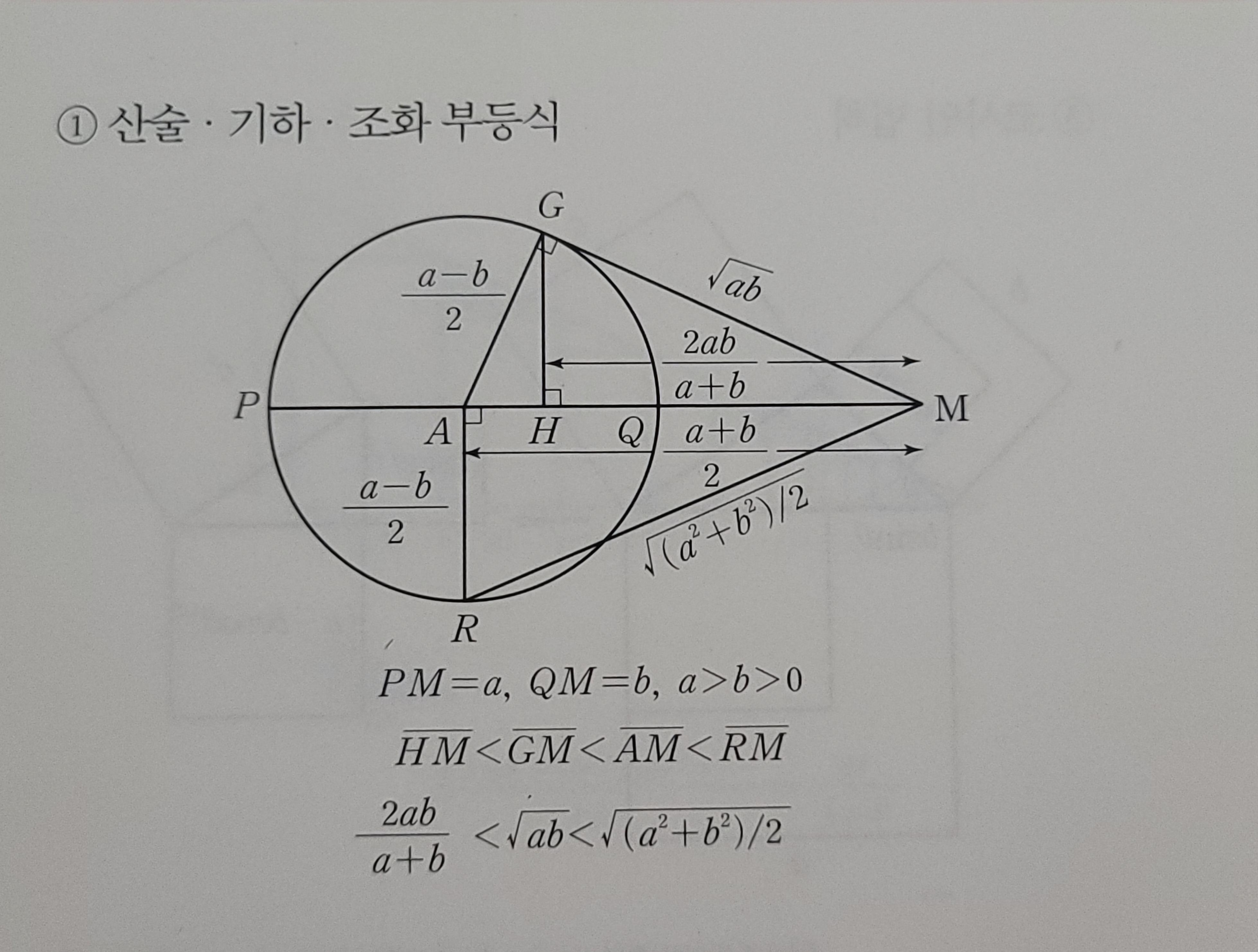
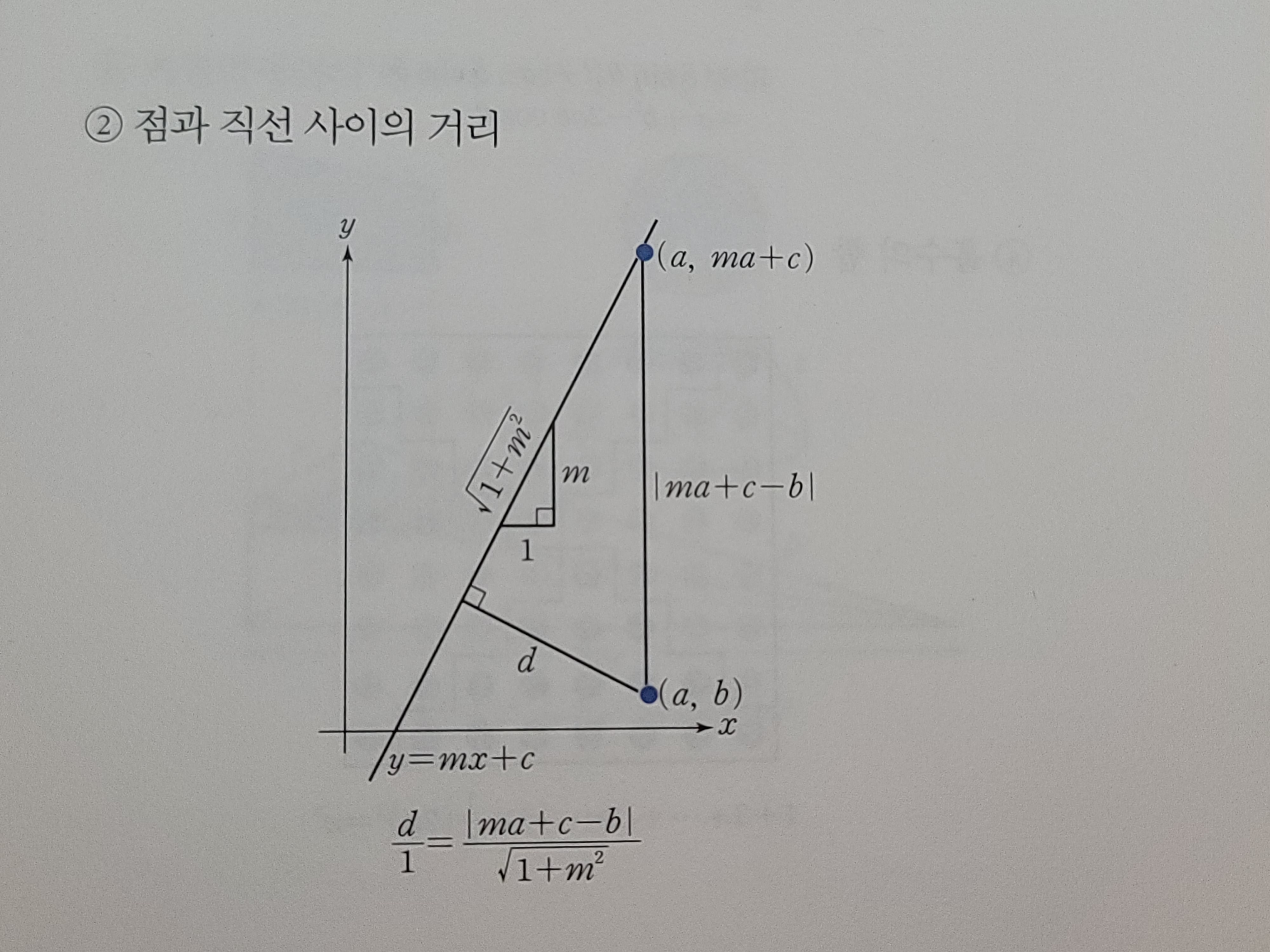
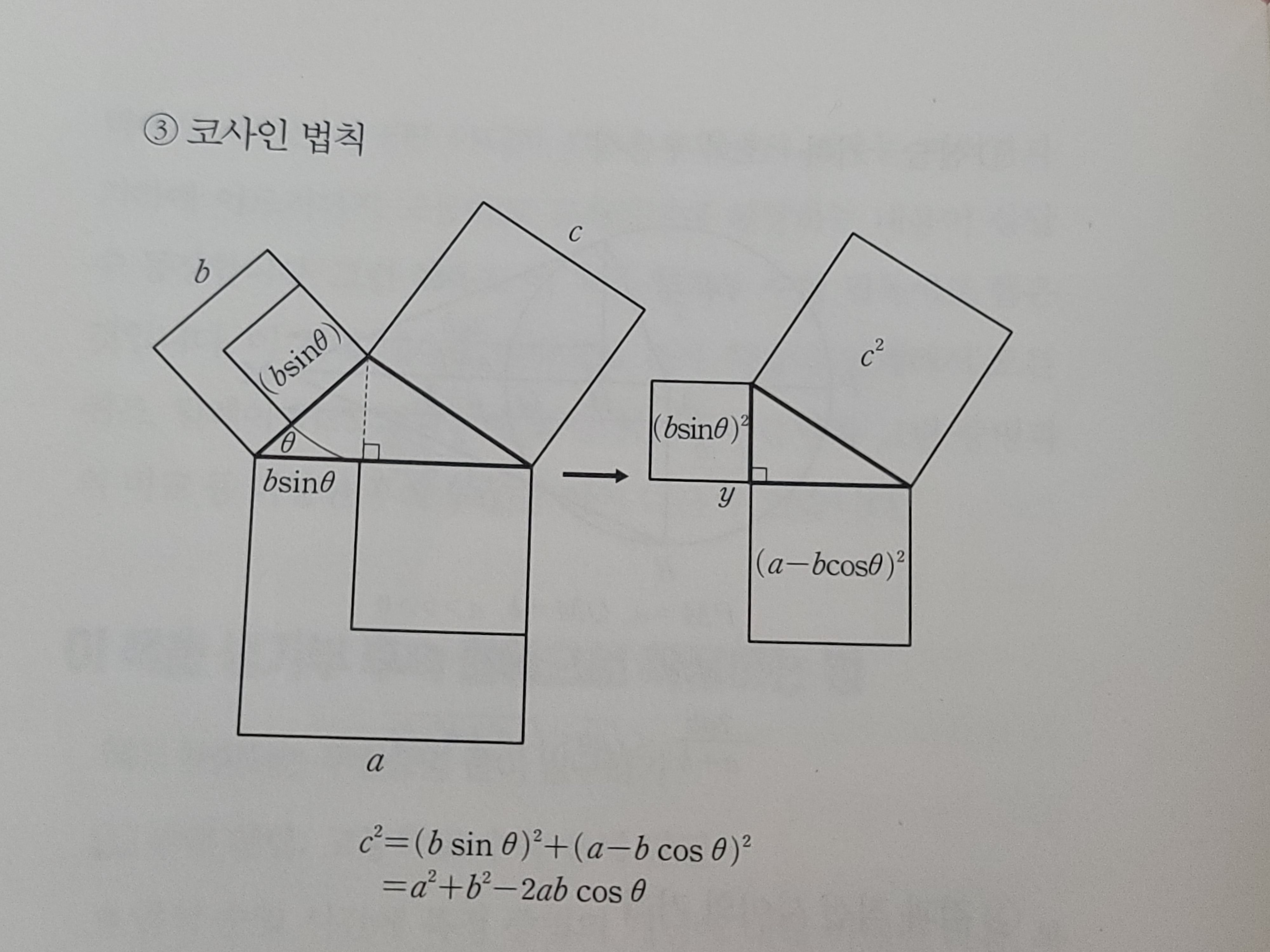
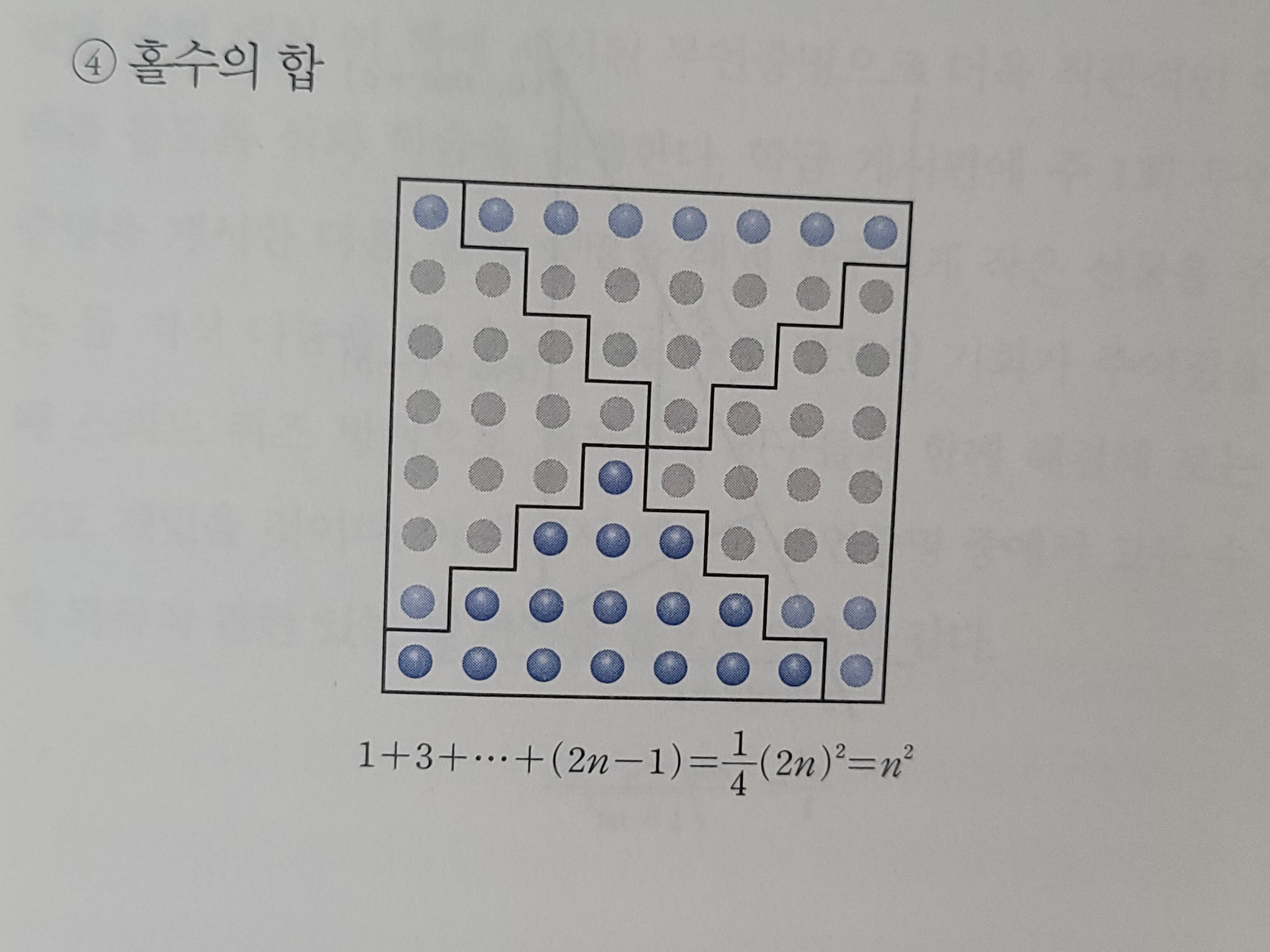
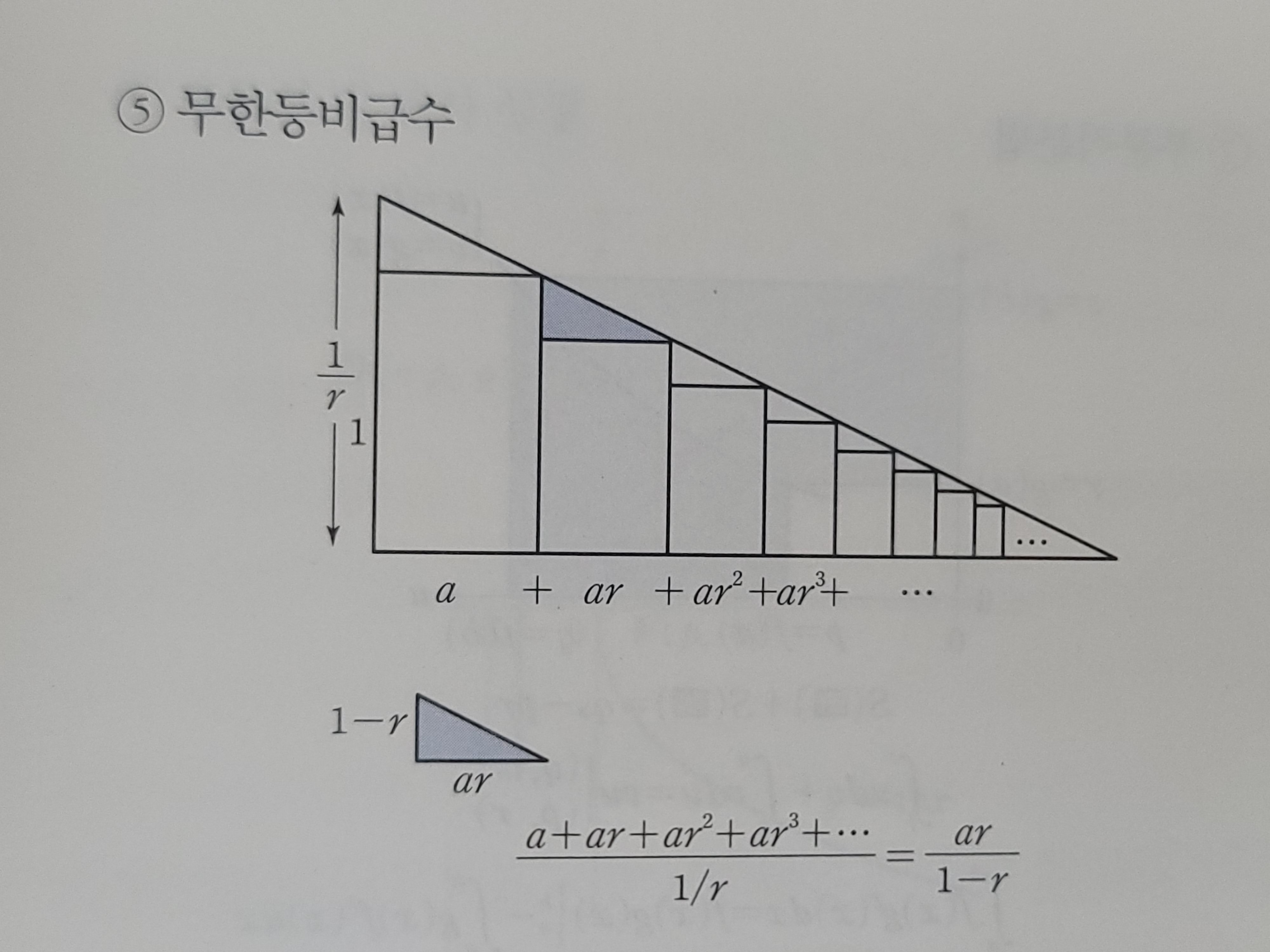
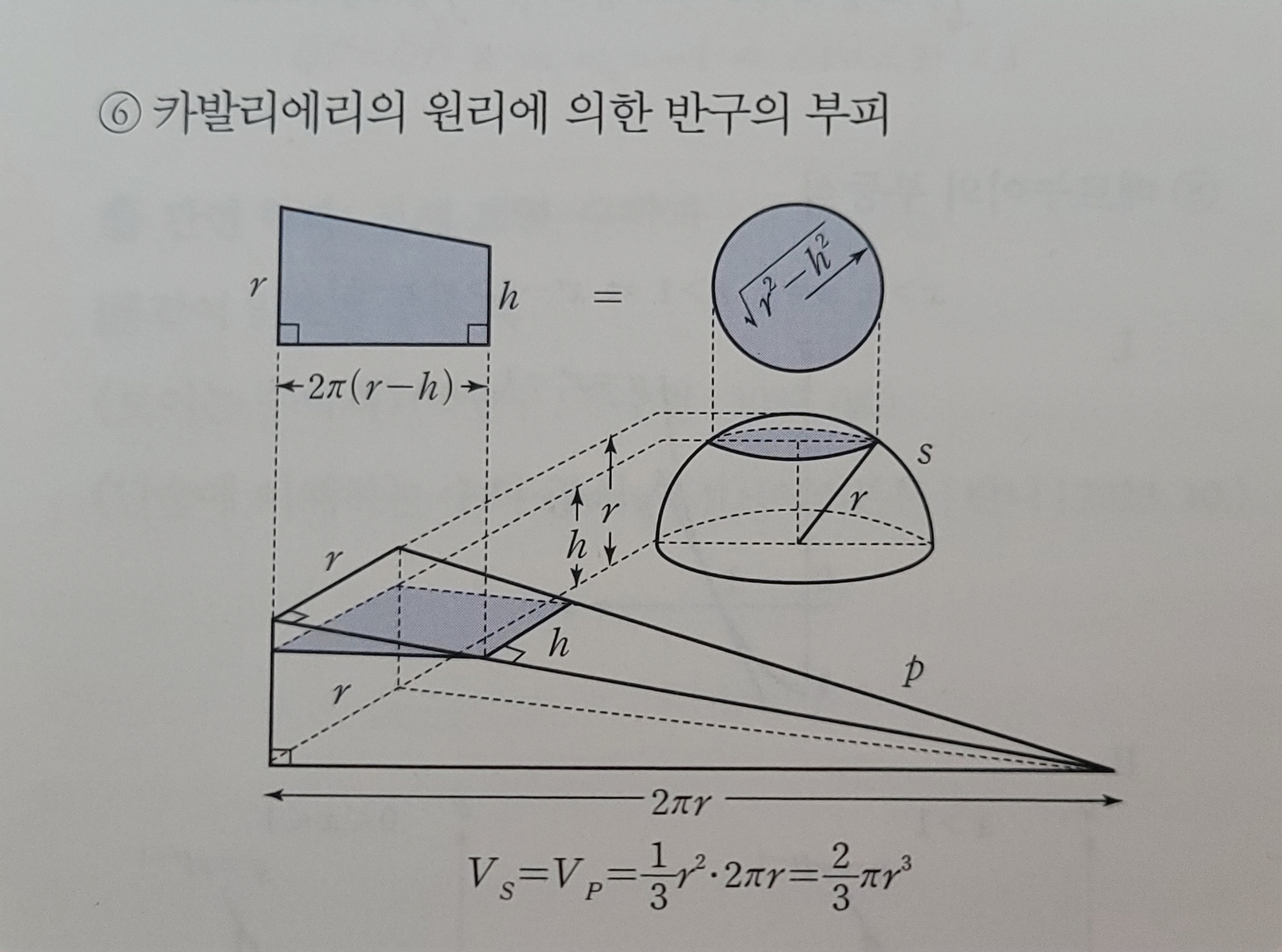
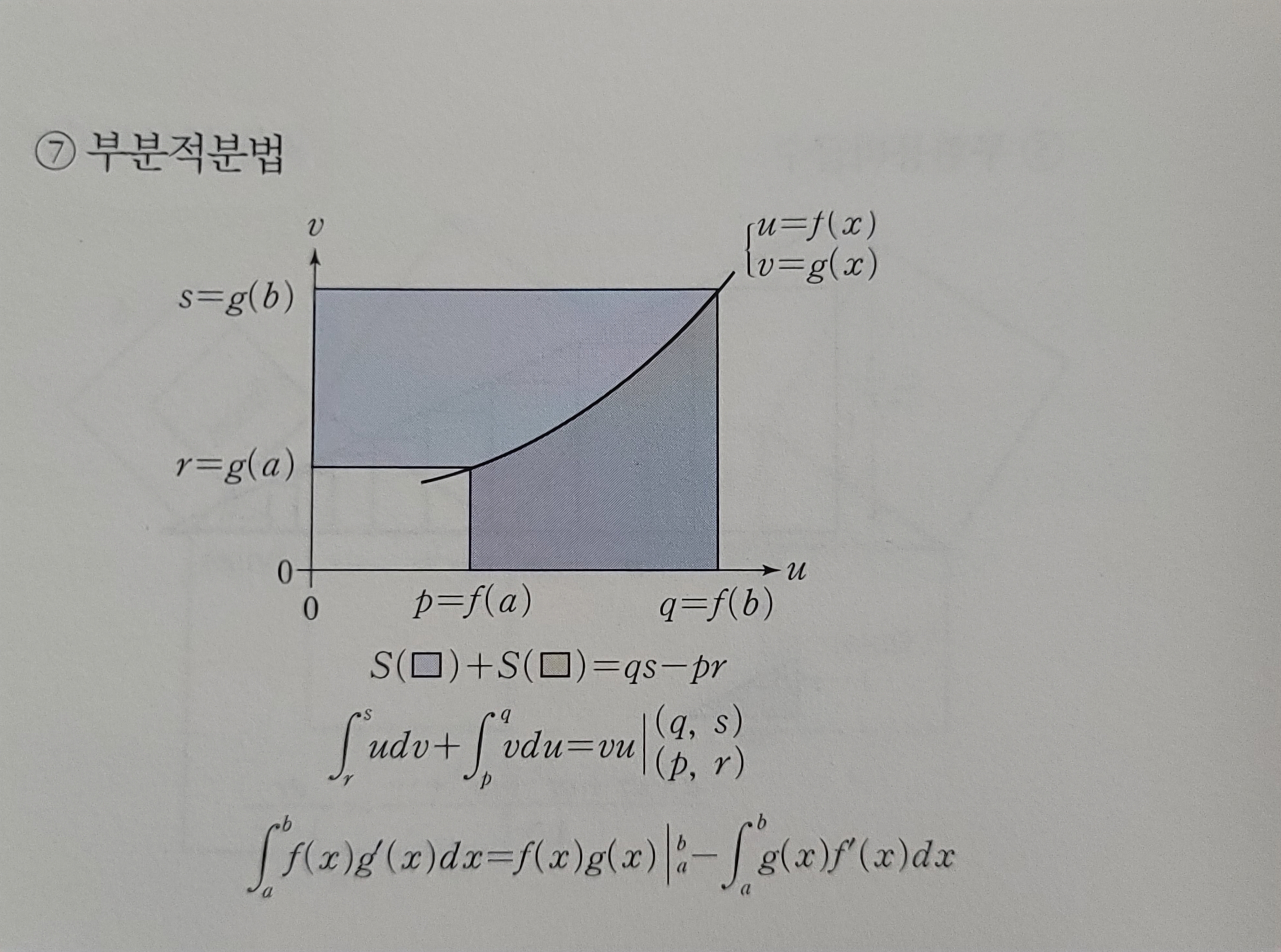
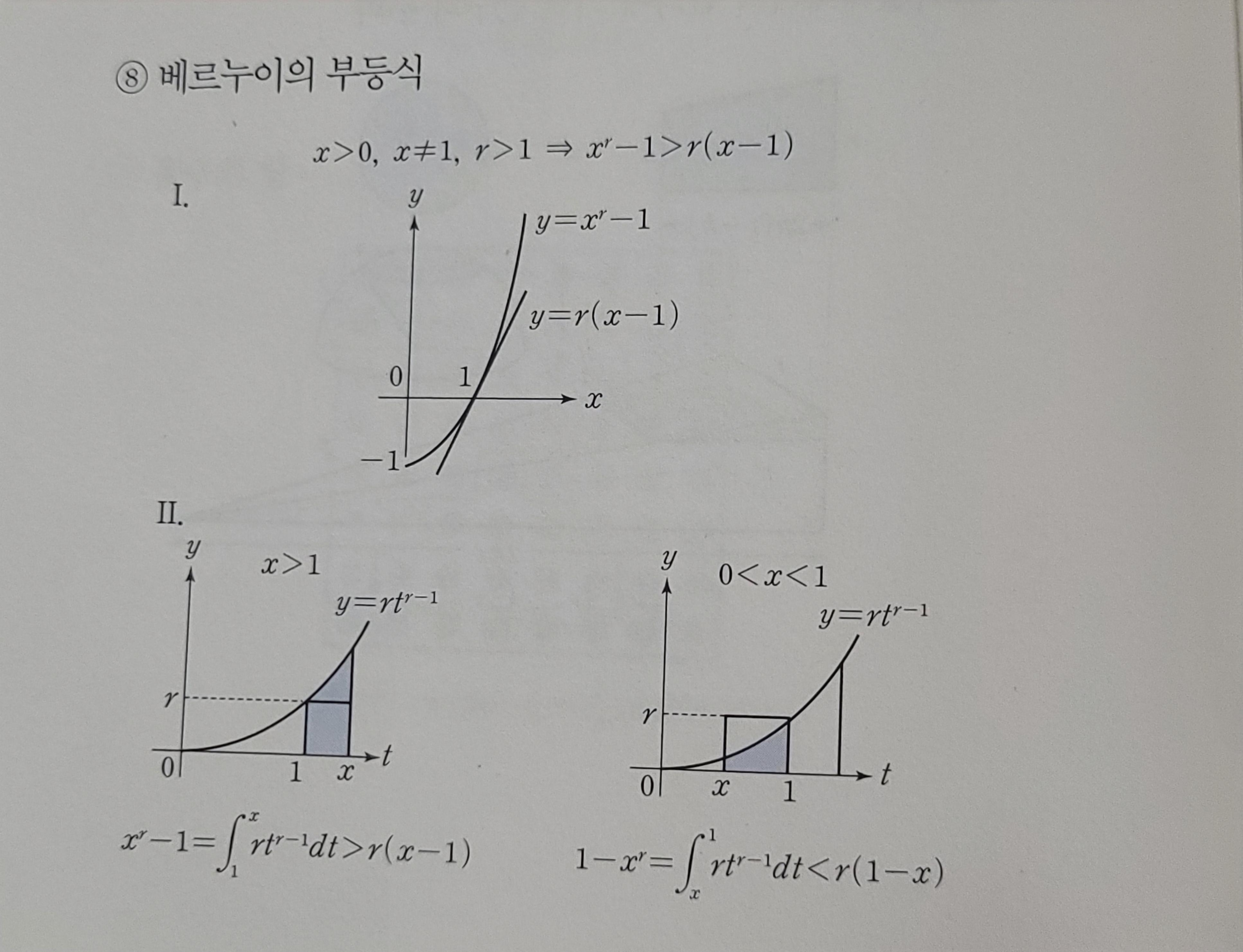
언제나 증명 하라고 하면
귀류법이나 대우 귀납등...이 생각 저생각 하며
어떻게 이끌어 내야 하나 고민 했는데...
무언증명 이라는 단어는 나에게는 정말 충격이었다...
시간이 날때마다....그림 하나하나 무언증명을 도전하며....첨삭챌린지 도전!!!☺️
#생기부 확장